三角形的光栅化

基础定义

视角（fov）

• 
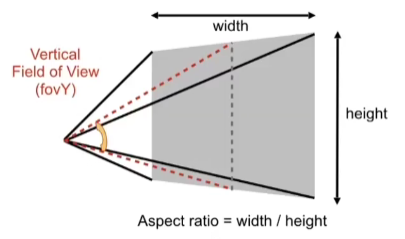
• 由视锥与近平面交接的平面会有宽度与高度，长宽比为$width/height$， 水平居中的线与相机组成的角为视角（Field of View）
• 

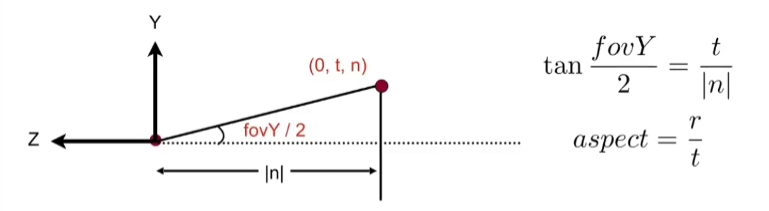
屏幕

• 图形学中认为一个屏幕是一个二维数组，数组的每一个维度的长度储存的是像素数量
• 屏幕坐标系定义左下角为$(0,0)$，并且使用下标表示每一个屏幕中的像素，像素的下标范围在$(0,0)$到$(width-1,height-1)$之间，像素的中心在$(x+0.5,y+0.5)$。屏幕的覆盖区域为$(0,0)$到$(width,height)$。

光栅化

• 在屏幕上绘制的过程称为光栅化

像素

• 像素在使用中会抽象成一个方块，内部不会有更多的变化，像素可能有不同的颜色或灰度。

视口变换

• 将一个三维的正方体渲染到图中，需要先进行是视口变化，由于正方体的大小为$2\times 2\times 2$且中心点在原点上，所以先将其缩放到视窗大小，并移动原点到左下角，具体变换矩阵如下

$$M_{viewport}=\left(\begin{array}{cccc}\frac{width}{2}& 0& 0& \frac{width}{2}\\ 0& \frac{height}{2}& 0& \frac{height}{0}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

三角形的光栅化

光栅化

• 需要判断屏幕上的每一个点是否在三角形内，如果在三角形内，则渲染颜色，否则则不渲染
• 一般计算的值为像素的中心，即对于$(x,y)$这个像素，计算的值为$(x+0.5,y+0.5)$
• 需要对每一个像素分别与三角形叉乘，如果得到方向一致，则可以认为该点在三角形内
• 如果点正好在三角形的边上，可以自己定义是否渲染
• 计算时可以不考虑三角形的包围盒(Bounding Box)外面的像素，这样可以节省大量开销
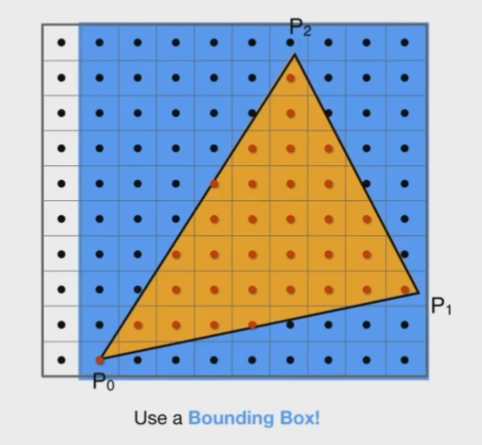
• 节省开销的时候也可以使用计算每一行三角形的最左与最右的包围盒
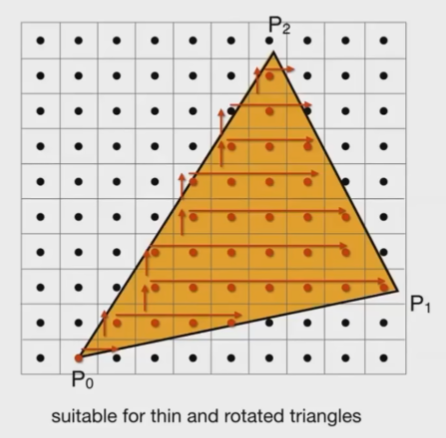
• 渲染结果类似 渲染结果会出现失真的效果，这种情况叫锯齿化，也叫走样(Aliasing)，如何解决锯齿化一直都是计算机图形学中的难题

反走样/抗锯齿

• 锯齿
• 摩尔纹

优化采样算法

模糊（Antialiasing）

• 先将三角形模糊操作，模糊后再采样，采样到的颜色为该像素颜色，可以有效反走样 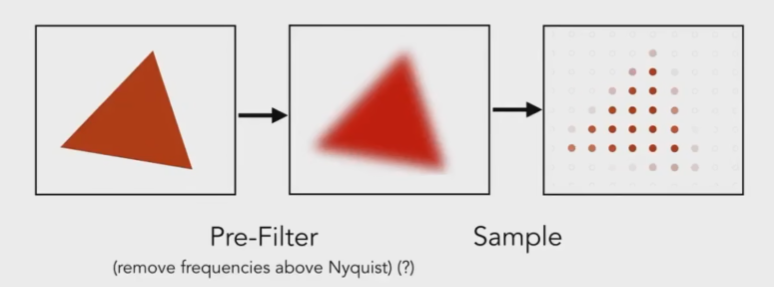效果： 需要先模糊再采样，而不能反过来先采样再模糊(Blurred Aliasing)。

滤波器

低通滤波器

• 将每个像素变成它与它周围像素的乘积后乘$\frac{1}{9}$ ，在亮度不变化的情况下将图像模糊

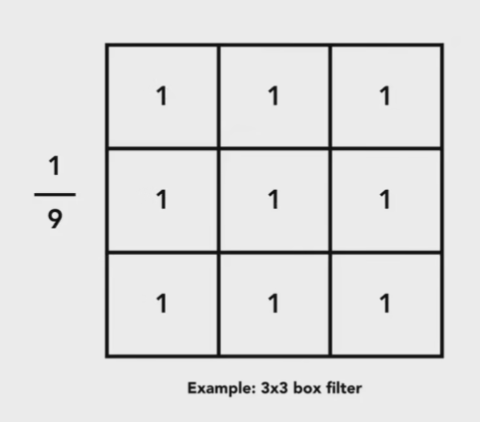
采样

• 时域上的乘积=频率上的卷积

反走样解决方法

• 增加采样率
• 模糊后再采样（模糊即将高频信号过滤掉后再采样）

MSAA

• 本来对于每个像素需要计算三角形在当前像素中的占比，并根据占比比例得出像素颜色。但是由于计算量过大，所以研究出了近似的MSAA方法。
• MSAA方法是在一个像素内多次采样的办法，它将一个像素分成了若干部分，分别判断是否在三角形内，最后得出结果
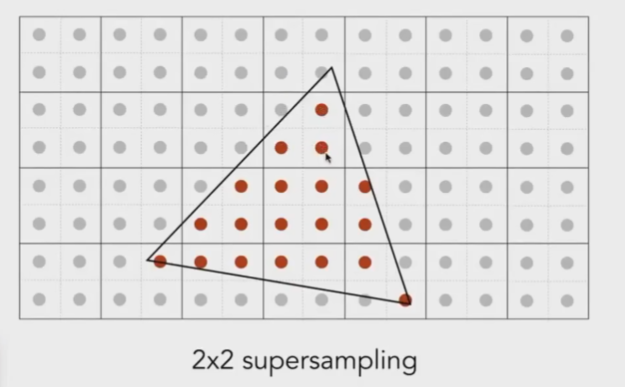
• MSAA是对图像的模糊的优化，而采样则由于最后得出了当前像素的颜色值，所以隐含了采样操作。
• MSAA是增加了计算量换来的显示效果，但是计算量大的情况下，得到的优化效果并未太大，所以工业中实现时一般不会使用将像素平均划分的方案，而是其他的采样方式，但思想相同。

其他的抗锯齿方案

• FXAA(Fast Approximate AA)快速近似抗锯齿，在正常采样后，通过高通卷积找到边缘，将边缘替换成无锯齿的方案。
• TAA(Temporal AA) 在时间上看如果该像素没有变化，则沿用上一帧的结果。

超分辨率(Super resolution)

• 将低分辨率的图像转化为高分辨率的图像时，会出现失真，所以需要优化
• DLSS(Deep Learning Super Sampling) 通过深度学习补全图像

可见性

• 如何保证视图中的三角形能保证顺序正确，遮挡正确
• 画家算法：先将远处的物体绘制完成，再绘制近处的物体将后面遮盖，但是对于一些互相遮盖的情况会出现问题

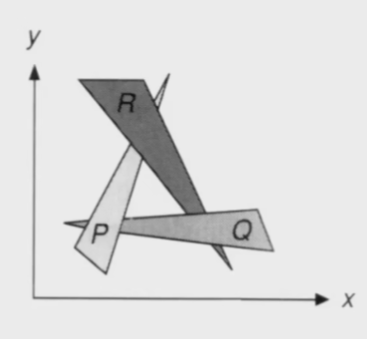
深度缓存(Z-Buffer)

• 存储每个像素中包含的几何中最浅的位置
• 即在生成图像时，需要同时生成两个图像，即渲染的图像(frame buffer)以及深度图像(deep buffer)
• 然后使用深度缓存维护图像的深度信息
• 实现